Going through all the articles on the web regarding privacy and hacking and the major role that cryptography plays in this arena, there was one specific concept that kept propping up again and again, and yet I never delved deep until a couple months back. Its the public-key cryptography scheme, thats based on the algebraic properties of elliptic curves over finite fields, more commonly known as elliptic-curve cryptography (ECC).

Turns out there are a bunch of cryptographic schemes/protocols that are based around this concept, and they are in wide use as of today, and in major applications/services that most people use everyday on the web. Now, I must admit that at this point I am in no position to comment on these protocols themselves but, just even barely scratching at the surface of this field of study I came across some pretty fascinating stuff.

Now if you are anything like me, one of the first questions that might have came up would be: What in the hell are elliptic curves Well naturally this question is actually pretty powerful and following its lead opens up the door to a whole array of concepts in algebra and number theory.

Elliptic curves in a general sense are cubic curves in two variables that are smooth, non-singular (no self-intersections, sharp bends/cusps or isolated points). The most general form for these set of cubic curves would be as follows:

\[Ax^{3} + Bx^{2}y + Cxy^{2} + Dy^{3} + Ex^{2} + Fxy + Gy^{2} + Hx + Iy + J = 0\]

With appropriate transformations using change of variables (I’ll try to cover it in another post later), this can be theoretically reduced to the following:

\[y^{2} = x^{3} + ax + b\] \[where; (a,b) ∈ \mathbb{R}\]

This is more commonly known as the Weierstrass equation for elliptic curves.

Now I must say that I have personally never come across such ‘weird’ equations for curves, after all I am spoiled by all those nice and simple quadratic equations . But it turns out that these ‘weird’ equations prop-up in an array of situations and mathematicians have been fascinated by them for a long time now. So I decided to plot one of these bad boys. And I get the following shape.

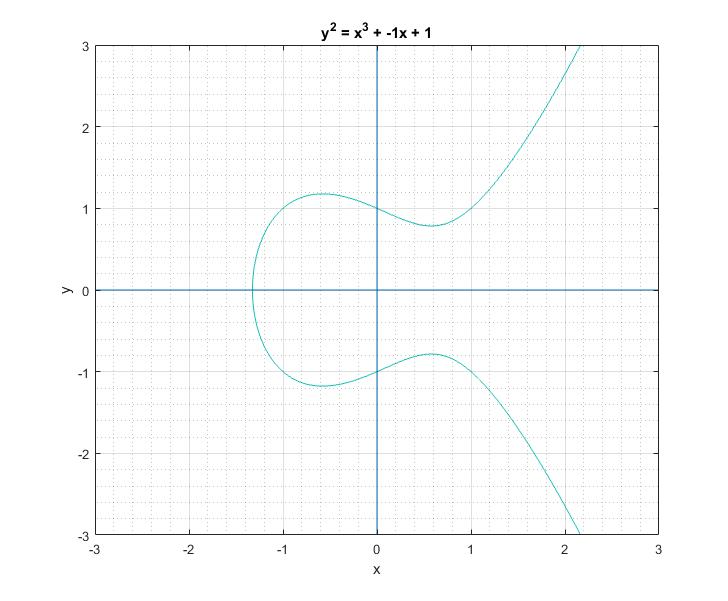
To a bystander that would clearly look like a rotated Lululemon logo, or the omega symbol. But as I learned, this is sort of a characteristic canonical look that these curves have. We can easily play around with the two parameters \(a\) and \(b\) of the Weierstrass equation and get a feel for what these curves generally look like. Following are some plots that I got.

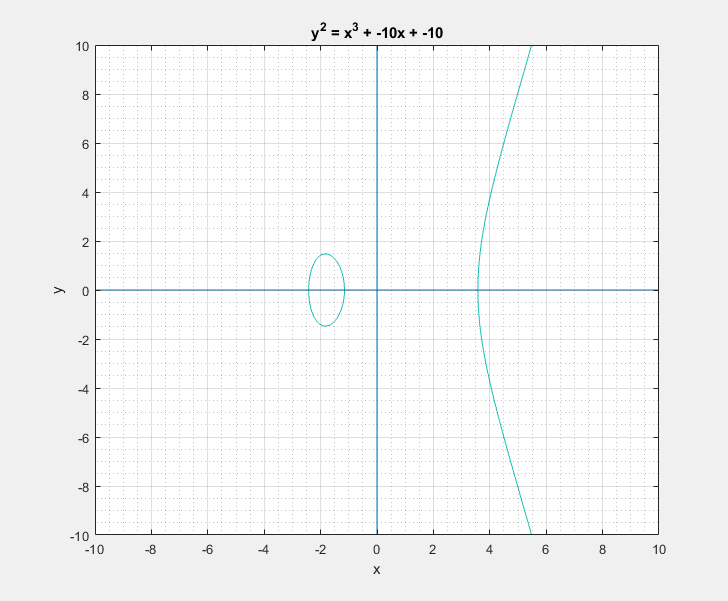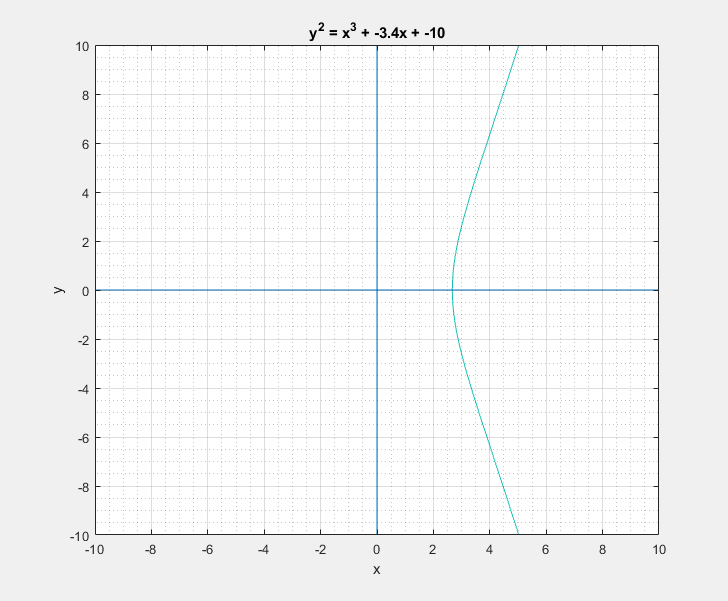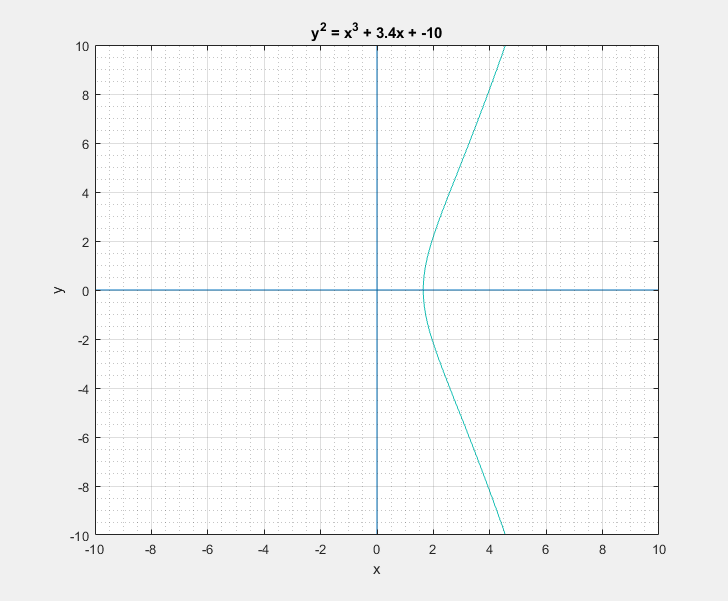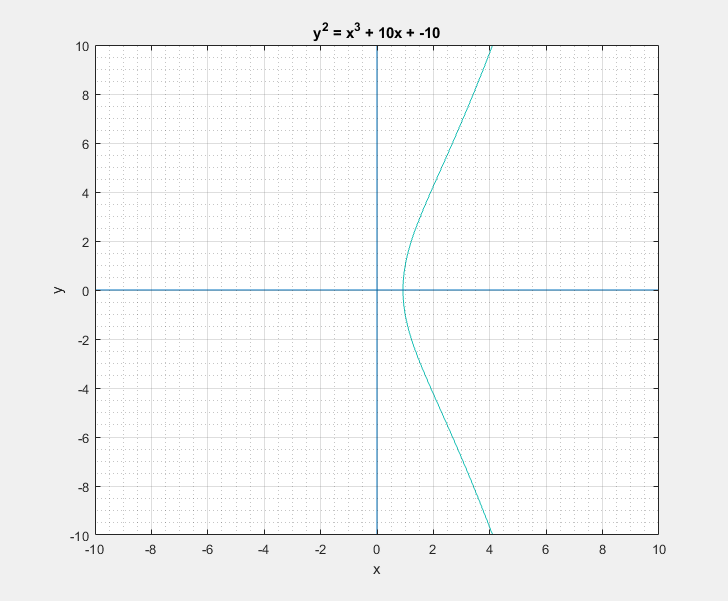
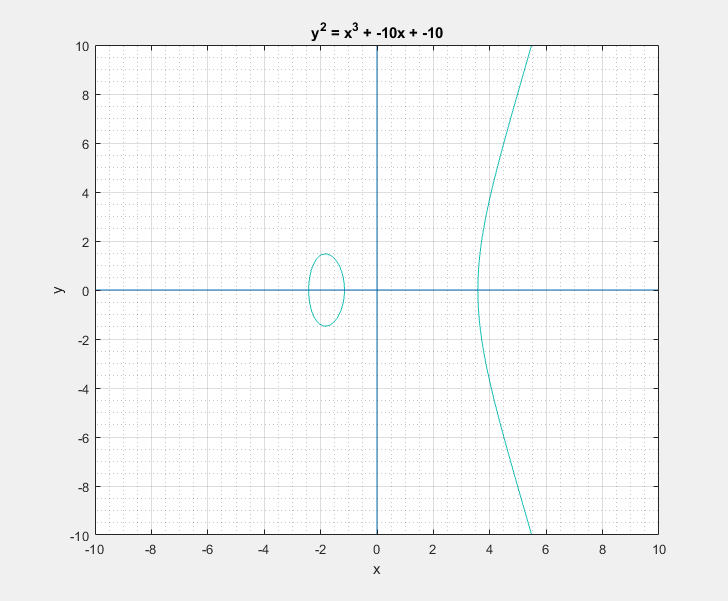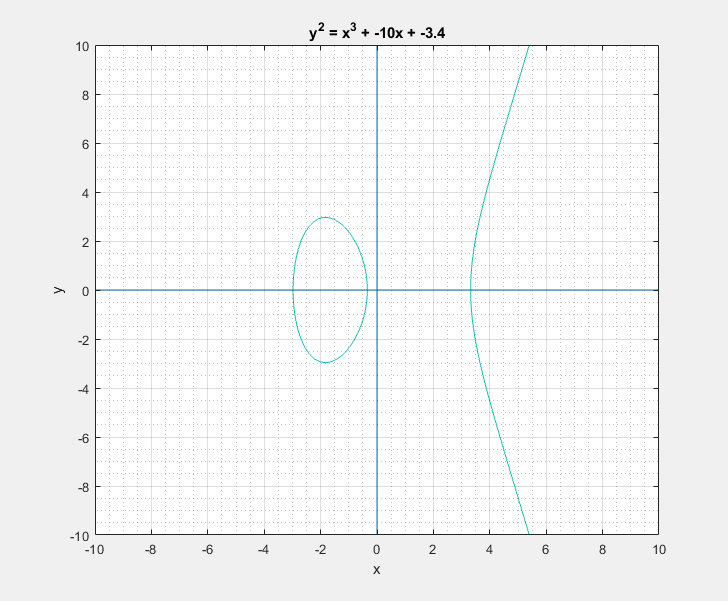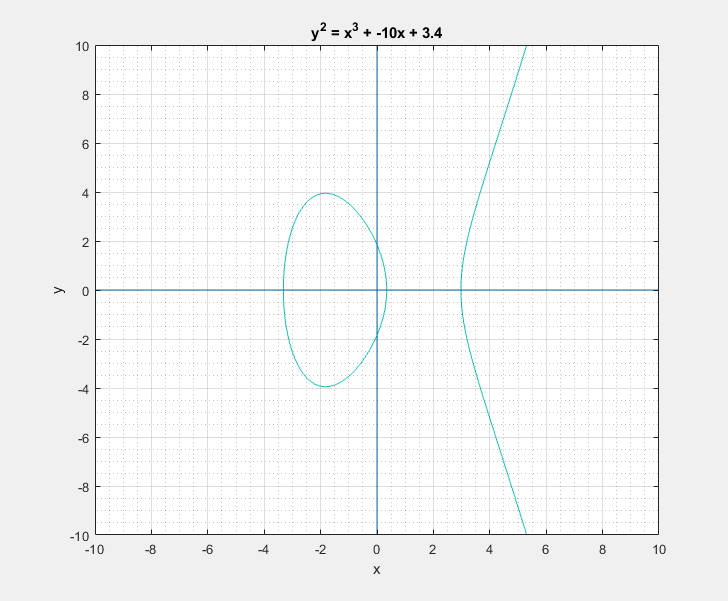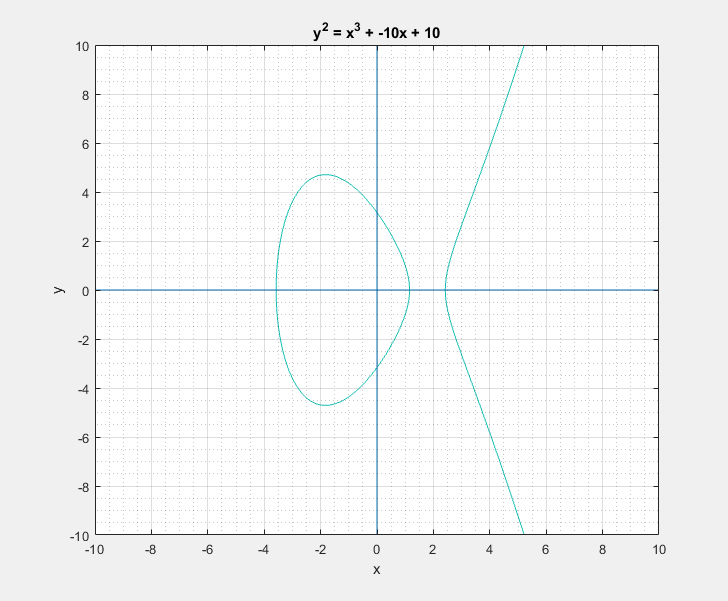
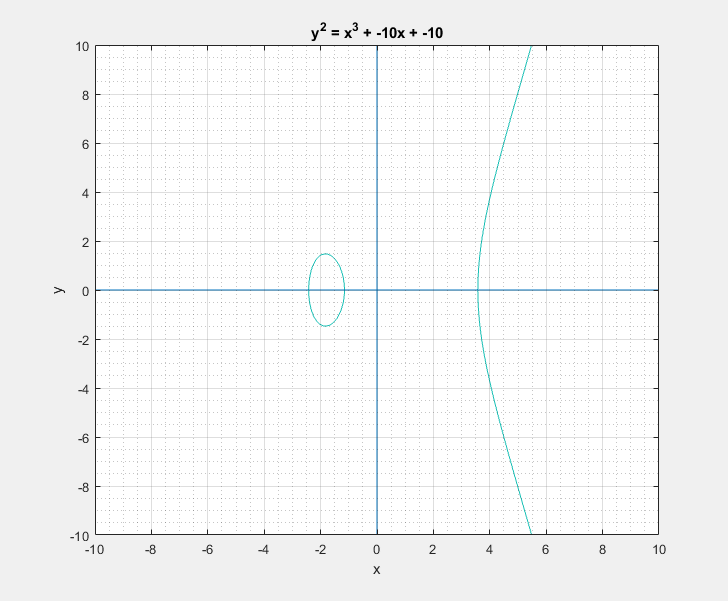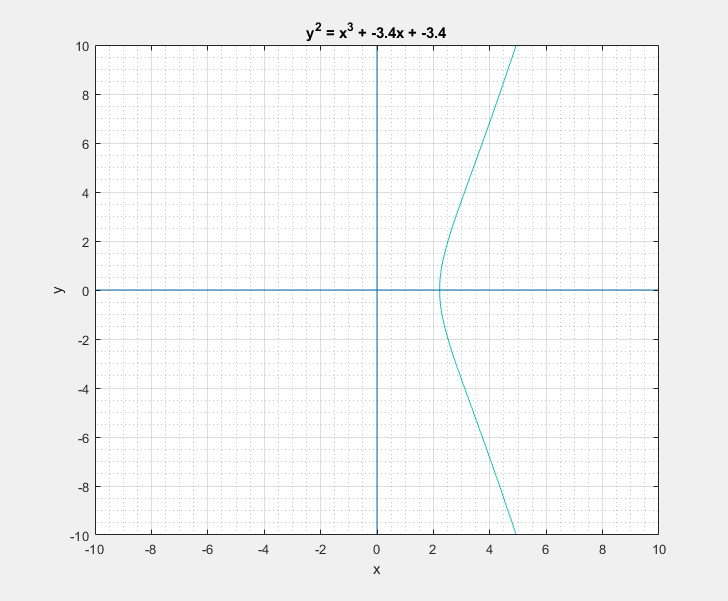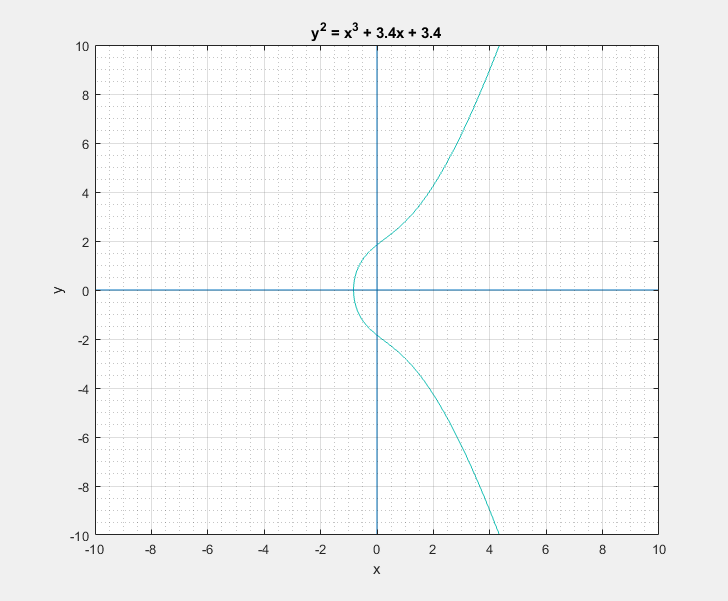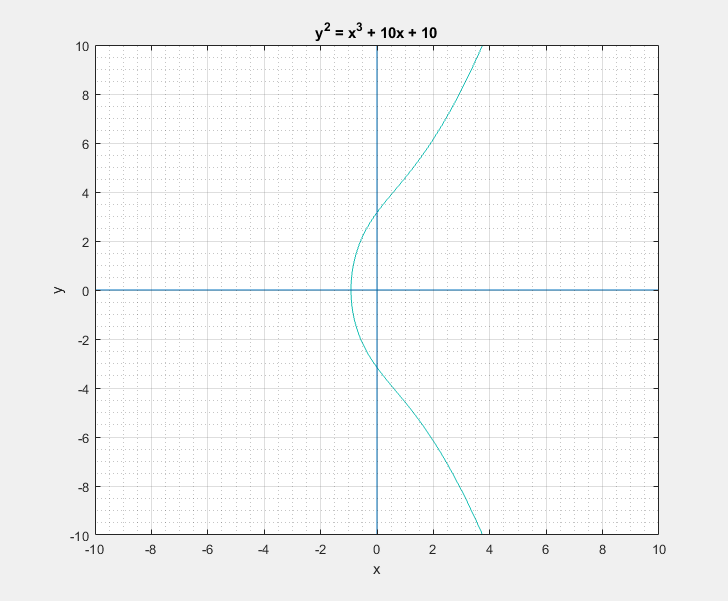
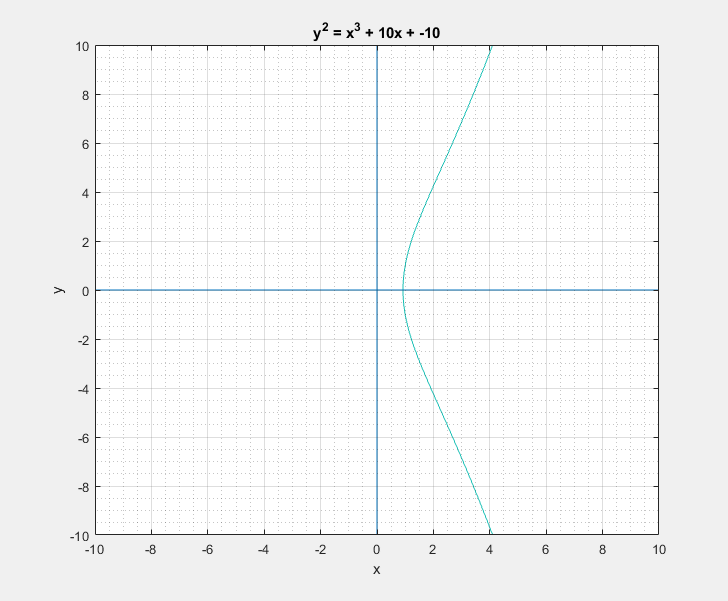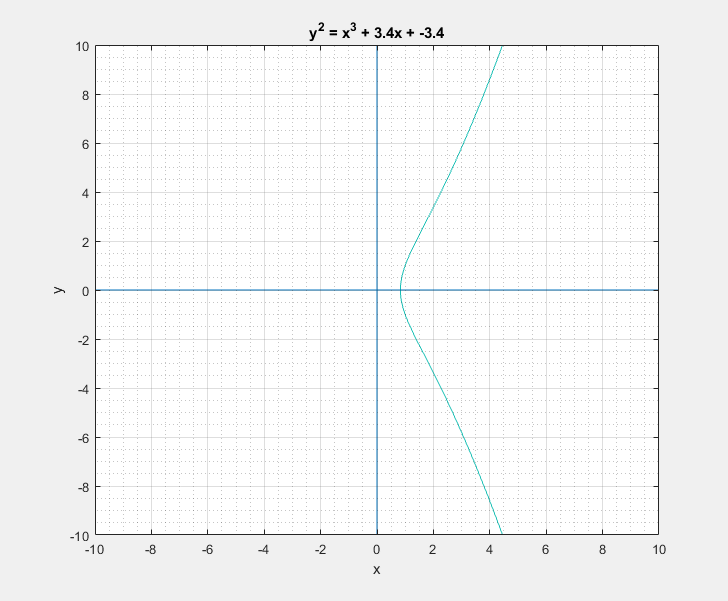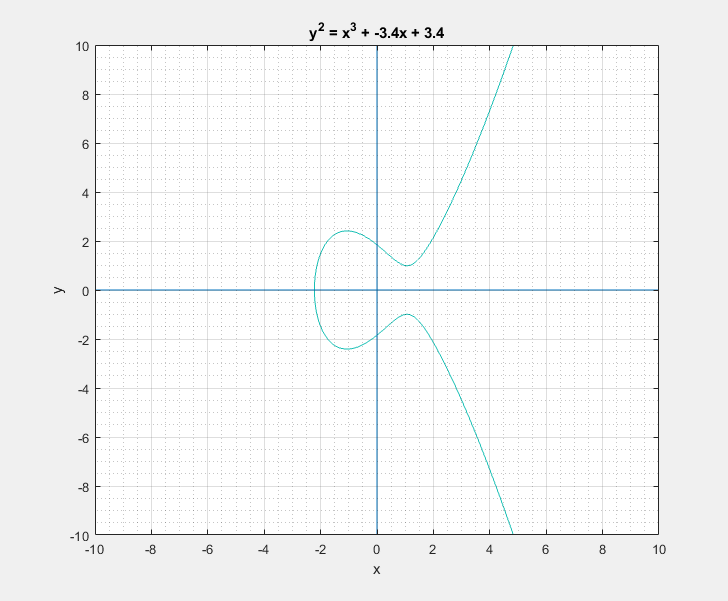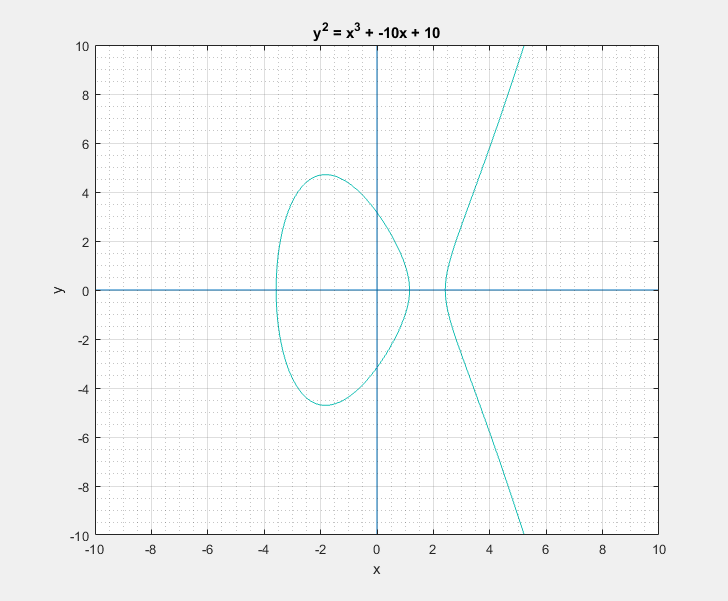
Now with all that said, another question that arises is: What is so special about these elliptic curves In short these elliptic curves, if defined with ‘appropriate’ set of additional edge condition rules, form a ‘Group’ which provides us with some very useful guarantees of handy algebraic properties in association with the overloaded addition/negation operators. In more formal terms elliptic curves form a commutative/abelian group, and gives us guarantees for the uniquenesses of the inverse and identity at all points on the curve among others. What that essentially means is that we are able to take a mathematical object (our curve) and perform a bunch of geometrical wizardry on it and still be able to define and perform them as algebraic operations with the associated operators.

Now this turns out to be perfect for applications within the world of cryptography, where we are always looking for Trap-door functions (something that is easy to compute one way, but very hard to reverse based on the output). The algebraic properties of elliptic curves make them very useful in this scenario, since our definition leads them to encompass logical structures within them, and we can check the efficiency of calculations within their computational structure in each direction. Turns out that we have the same Discrete Log Problem (DLP) within this algebraic structure with certain conditions. And, this computational difficulty is what essentially is at the base of all the security that is provided by the elliptic-curve cryptographic schemes.

And so I guess these ‘Weird’ curves are indeed super handy!

TL;DR

Elliptic curves are the backbone of major public-key cryptography schemes, and are strongly backed by a lot mathematical research and industry applications over the last few decades. The precise and powerful algebraic group properties of these curves make them perfect for applications requiring strong trap-door functions and efficient computation capabilities.